
С помощью шести спичек построить три одинаковых квадрата. Требуется немного нестандартного мышления.
Ответ: Извините за то, что ответ выглядит несколько издевательски, но мы ведь не говорили, что нельзя ломать спички.
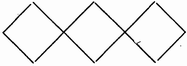

С помощью шести спичек построить три одинаковых квадрата. Требуется немного нестандартного мышления.
Ответ: Извините за то, что ответ выглядит несколько издевательски, но мы ведь не говорили, что нельзя ломать спички.

Комментарии
можно решить не ломая спички, правда при этом остаются лишние концы,решение очень простое - строите квадрат из 4 спичек, назовем, его А, 2 оставшиеся спички помещаете внутри квадрата А друг на друга, так чтобы те разделяли квадрат А на четыре маленьких квадрата. Теперь мы имеем 4 квадрата, остается избавиться от одного, - сдвигаем одну из спичек, образующих стороны квадрата А на половину длины - имеем три квадрата.
браво 37 я тож также решил. А вообще как было замечено чтоб не чуствовать себя идиотом. Следовало бы в задачу вводит доп требования например Квадраты д.быть Максимальны по площади!
браво 37 я тож также решил. А вообще как было замечено чтоб не чуствовать себя идиотом. Следовало бы в задачу вводит доп требования например Квадраты д.быть Максимальны по площади!
Хотя Забавно-с. наши-то с тобой придумки По параметру площадь нисколько не уступают квадратам приведённым в решении!!!
А Вот по параметру материалоёмкость, и трудоёмкость выглядят даже более выиграшно.Т.к. экономят в сумме целую спичку. Слава Горбачёву М.С. "Экономика должна быть экономной"
если издеваться - то можно и так:
пристроить две спички к углу стола (т.е. этот самый угол будет образовывать две другие стороны квадрата). Затем к любой стороне первого квадрата пристраиваем ещё две спички - 2 квадрат и тэ дэ, насколько хватит коробка ))
а вы попробуйте, не ломая, из 6 спичек сложить 4 одинаковых треугольника...
из 6 спичек - 4 одинаковых треугольника":
решение 1 - Из 3 спичек складываем равносторонний треугольник. В каждый угол помещаем по спичке и свободные концы соединяем вместе, образовывая пирамиду из 4-х равностороних треугольников.
решение 2 - кладем 2 спички накрест посередине их длины, образовывая прямой угол. Остальные 4 образуют квадрат (будут торчать "хвостики"). 4 треугольника образованы пересечением диагоналей квадрата.
Согласен. Но вы ведь не говорили, что нельзя накладывать спички друг на друга, и чтобы концы спичек не торчали. Вот решение:
__________
| |
|____|____
| | |
|____|____|
|
|
Не ломая, но накладывая:
Кладем 4 спички параллельно друг другу (IIII)? расстояние между ними должно составлять 0,25% от длины спички.
Двумя оставшимися спичками пересекаем, указанные 4 (=), при этом расстояние между этими двумя также 0,25% от длины спички.
В итоге получаем сетку, внутри которой 3 одинаковых квадрата.
P.s. Не подумайте, я не пол года думал... просто открыл этот ресурс для себя пару дней назад и только сейчас дошел до этой задачи.
Ошибочка... Не 0,25%, а треть от длины спички.
Если сломать все спички пополам, любой олигофрен сможет построить!
это в точку)))
Извините, но в ответе не квадраты, а ромбы ))
да-да-да!!!37# полностью с тобой согласен!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Юмористы, блин.
Любой квадрат является ромбом. И никакой квадрат не перестаёт быть квадратом из-за того, что его повернули на 45 градусов :)
Упс, это был ответ на предыдущий коммент :) ("...в ответе не квадраты, а ромбы")
Есть наилучшии вариант. Можно построить сломав одну спичку и наложить спички один раз!
|
______|
| | |
|__|__|
| |
__|__|
|
|
|
| - 1 спичка. И ломать ничего не надо.
Пробелы впереди не получилось поставить.
___
|_|_
|_|_|
|
|
| одна спичка и _ _ одна спичка
криво вышло, пробую переделать:
___
|_|_
|_|_|
......|
____
!__!__
!__!__!
!
можно составить квадрат из 4-х спичек, внутри разместить крестом ещё две. Получится 4 равных квадрата.
второй вариант-разместить спички в пространстве таким образом, что бы проекции на координатные плоскости давали квадраты. в этом случае, получается даже 6 равных квадратов-проекций. В конце-концов, никто не говорил, что нельзя использовать клей.
Никто не говорил, что спички не могут выходить за края квадратов. Вот помоему реальный ответ. А если можно сломать - то не обязательно пополам. Тогда из них и "розочку" можно выложить :)))
_____|
|__|__|
|__|__
Считаю этот ответ наиболее правильным и изящным.
А меня также получилось)))
+1
_____|
|__|__|
__|__|
У меня получился ответ не ломая спички....
____
I_I_
I_I_I
I
Не ломая спичек
1 ______
2 |__|__
3 |__|__|
4 |
5
Поправка, а то текст не редактируется
зачем ломать? просто из 4 построить один квабрат большой и внутри его две оставшиеся спички крестом положить.) получается 4 маленьких одинаковых квпдрата внутри большого
А мы сделали так:
_ _
|_|_|
|_|_|
Три одинаковых квадрата выходит, каждая спичка состоит из двух частей, потому что непрерывную не нарисуешь (мы их честное пионерское не ломали!).
и не испорчена ни одна спичка :) А у нас дома гаааз :)
Балин, ёкарный бабай, звиздецный патефуй, шоб их всех перекорячило, да юзом обормотило:
поправка!
_ _
.|_|_|
.|_|_|
. - это глюк! протрите экран монитора :)
а у кого ноуты - просто экран :)
а кто 4 квадрата сделал??
4 это слишком просто
так чо, мне тогда 1 спички хватит, еще останется. а я уж начал было думать, что решение вообще надо искать в неевклидовом пространстве. и это называется нестандартное мышление? хаха
Если ломать спички, то можно много вариантов предложить. На самом деле формулировка задания подкачала, надо добавить - три одинаковых квадрата максимальной площади.
вы так же не говорили - что нельзя зделать более 3х квадратов.
можно сложить четыре спички в квадрат и разделить их крестиком.
А ломая спички можно сколько хочешь квадратиков наделать.
Я сразу догадалась, 3 квадрата 12 спичек) 6 разделить на половины.
По-моему, изящнее следующий ответ:
спички выкладываем таким образом (зигзагом с прямыми углами):
/\/\/\
и к нижней стороне зигзага приставим зеркало:
/\/\/\
\/\/\/ получим тот же рисунок, что в ответе у автора, но частично иллюзионный))
Раз можно ломать спички,нужно сломать все пополам (6*2=12) для одного квадрата понадобиться 4 половинки (12/4=3) и получается как раз 3 квадрата
можно не ломая спичек
Можно, не ломая спичек
_ _
х|_|_
х|_|_|
хххх|
вот как-то так (одна спичка = две линии, а крестики чтобы не съезжало). Это если домыслить, что квадратов должно быть НЕ БОЛЬШЕ трех. Если же можно больше, то сделать один квадрат и перекрестить его внутри - получится 5. А если ломать, можно хоть миллион квадратов сделать.
Вопрос поставлен некорректно, не верю, что это из Менсы.
У меня было 2 ответа - сломать спички и построить три квадрата так, что половинки двух спичек не являлись бы сторонами квадратов (если можно ломать спички, то почему нельзя с ними поступить и так?).
ахаха))) не ну у меня было предположение, что надо сломать спички, но я не думала что они так прикалываться будут)))) супер!)))
Попробовал два не стандартных вариант
1) в ЗД
2) "мини" квадратик в этой фигуре: _I_
I
ни там,ни там у меня ничего не вышло,потому я пошел ломать спички,хотя не хотел использовать этот способ. но условий нигде не было,потому вариант с ломанием - верный.
можно не ломать 4 по вертикали положить а 2 по горизонтали в центре 3 равных квадрата
Ломать не обязательно. Выкладываем квадрат, внутри него крест из 2х спичек. получаем 4 квадрата, вернее даже 5 считая 4 малых и 1 большой, теперь смещаем одну из сторон большего квадрата до половины и остается 3 полных малых квадрата со стороной 1/2 спички.
Задача с юмором и в условии не сказано что кроме квадратов у нас не должно остаться ничего, в том числе и выступающих спичек.
А если, как у них ломать спички пополам, то можно обойтись и 5ю.
________|
| | |
|___|___|
| | |
_|___|_
Ну вот как-то так, если не ломать. А если поломать, то можно и больше сделать, тогда вообще идиотизм какой-то
Страницы