На этом рисунке 4 человека, двое из них в черных шляпах и двое - в белых.
Перегородка - это стена, через которую ничего не видно.
Слева направо: 1-й человек видит 2-го и 3-го, 2-й видит 3-го, 3-й видит стенку, 4-й вообще ничего не видит.
Они знают, как они стоят, знают, что есть 2 черные и 2 белые шляпы.
Каждого из них спрашивают: "Знаешь ли ты, в какой ты шляпе?"
Допускается два варианта ответа: "Да, знаю, я в ... шляпе" либо "Нет. Не знаю"
Кто первым сможет ответить, в какой он шляпе?
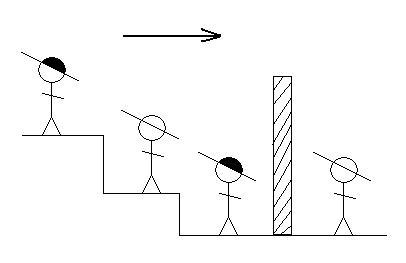
Ответ: Второй.

Комментарии
Второй!
Почему?
2-й видит на 3-ем черную шляпу и рассуждает так: Если бы на мне была черная шляпа то 1-й, видя перед собой (на 2-м и 3-м) две черные шляпы, сразу бы крикнул что на нем белая шляпа, а так как он молчит, следовательно на мне (2-м) белая шляпа.
Они же знают как они стоят. Первый видит перед собой белую шляпу, а за ней - черную. И зная, что они чередуются, знает, что он в черной шляпе. И отчего второй должен слышать ответ первого? Если решение основано на том, что они слышат друг друга, то стоило бы это как-то упомянуть в условии.
он не знает, что они чередуются, по крайней мере об этом в задаче не сказано. Сказано лишь то, что они знают что и черных и белых по две штуки. Первый увидит 2 разные шляпы, значит не возможно сказать, какая на нём. он скажет, что не знает. 2-й услышит это и поймет, что если бы на нем была та же шляпа что и на 3-м, то 1-й бы точно знал, какая шляпа на нем. Но он не знал, значит второй поймет и скажет , что на нем шляпа, противоположная по цвету чем у 3-го
ТАК КАКОЙ ОТВЕТ ВЕРНЫЙ?
Верный ответ — тот, что привёл автор.
Объясню, почему.
На начальном этапе никто из них не знает, в какой он шляпе. 4-й в принципе не может изначально знать, в какой он шляпе. Третий тоже. И второй. А вот первый мог бы знать, в какой он шляпе, если бы у второго и третьего шляпы были бы одного цвета. Например, если бы второй и третий были бы в белых шляпах, третий бы знал, что он в чёрной. Но третий не знает, потому что второй и третий в шляпах разного цвета.
Когда все услышат, что 4-й не знает, в какой он шляпе, это никому ни о чём не скажет, так как 4-й и не может знать, в какой он шляпе. Когда все услышат, что 3-й не знает, в какой он шляпе, это опять никому ни о чём не скажет. То же самое и насчёт второго. Но когда первый скажет, что он не знает, в какой он шляпе, то всем сразу станет ясно, что на втором и третьем — шляпы разного цвета.
После того как все это осозна?ют, случится следующее. Четвёртый, осознав это, так и не узнает, в какой он шляпе. Третий тоже: хотя он и знает, что на нём шляпа не такая, как на втором, но он не знает, какая на втором, так что он тоже не узнает, какая на нём. Четвёртый — ясное дело — тоже не узнает, так как он и раньше знал, какие шляпы на 2-м и третьем, так что от того, что он скажет: «Я не знаю, какая на мне шляпа» — он не узнает вдруг, какая же. А вот второй, как только услышит, что первый не знает, какая на нём шляпа, сразу поймёт, что на нём само?м (на втором то бишь) не такая шляпа, как на третьем. Так что второй тут же поймёт, что на нём белая шляпа, и скажет об этом. Это и есть ответ задачи.
После этого третий поймёт, что раз на нём не такая шляпа, как на втором, а на втором белая, значит, на нём чёрная, и тоже скажет об этом.
Первый и так это знал, так что ему от этого не станет ясно, какая шляпа на нём. А пока первый не узнает, не узнает и четвёртый. Так что ни первый, ни четвёртый так и не узнают, какие на них шляпы. НИКОГДА.
Точнее, пока не снимут их и не посмотрят. :) Вот так.
Итак, верный ответ — второй раньше всех узна?ет, какая на нём шляпа.
Затем третий узна?ет. А первый и четвёртый — никогда не узна?ют.
Согласен. Есть ответ.
Замечательная задача! Самое интересное, что действительно всё решается логически - без всяких перелезаний через стену и сниманий шляп :)
никто ответить не сможет
четвертый ничего не видет, следовательно чужие ответы ему не дают новой информации
с третьим такая же ситуация
теперь первый и второй
только первый обладает максимумом информации по ситуации, но она ему ничего не дает также, все что он знает - что впереди черная и белая. чужие ответы дополнительной информации не дают.
второму также не легче - он не знает распределение шляп по цвету между стенкой. ответить утвердительно на вопрос о цвете шляпы можно только наблюдая трех оставшихся
4 его се ровно невидно он может снять посмотреть =))) ,или 2 он может назад посмотреть !!!
"2й" видит только 3го, и знает что первый видит и его и 3го , и видя что на третьем черная шляпа он поймет что если бы на нем тоже была черная шляпа то 1й сразу сказал бы что на нем белая, так как он этого не сделал , 2й понял что на нем белая шляпа
второй
Молчание это тоже информация.
Блин. Жаль, на этом сайте нельзя исправить собственную опечатку. В моём комментарии опечатки! Привожу исправленный вариант (надо было сначала исправить, а потом уж сохранять, а я — балда — всё наоборот делаю). Ну что ж, лучше поздно, чем никогда. Опечатки — и дополнения — выделю форматированием.
Верный ответ — тот, что привёл автор.
Объясню, почему.
На начальном этапе никто из них не знает, в какой он шляпе. 4-й в принципе не может изначально знать, в какой он шляпе. Третий тоже. И второй. А вот первый мог бы знать, в какой он шляпе, если бы у второго и третьего шляпы были бы одного цвета. Например, если бы второй и третий были бы в белых шляпах, первый бы знал, что он в чёрной. Но первый не знает, потому что второй и третий в шляпах разного цвета.
Когда все услышат, что 4-й не знает, в какой он шляпе, это никому ни о чём не скажет, так как 4-й и не может изначально знать, в какой он шляпе. Когда все услышат, что 3-й не знает, в какой он шляпе, это опять никому ни о чём не скажет. То же самое и насчёт второго. Но когда первый скажет, что он не знает, в какой он шляпе, то всем сразу станет ясно, что на втором и третьем — шляпы разного цвета.
После того как все это осозна?ют, случится следующее. Четвёртый, осознав это, так и не узнает, в какой он шляпе. Третий тоже: хотя он и узна?ет, что на нём шляпа не такая, как на втором, но он не знает, какая на втором, так что он тоже не узнает, какая на нём. Четвёртый — ясное дело — тоже не узна?ет, так как он и раньше знал, какие шляпы на 2-м и третьем, так что оттого, что он скажет: «Я не знаю, какая на мне шляпа» — он не узнает вдруг, какая же. А вот второй, как только услышит, что первый не знает, какая на нём шляпа, сразу поймёт, что на нём само?м (на втором то бишь) не такая шляпа, как на третьем (ведь если бы на втором была такая же, как и на третьем, первый бы знал, что на нём другая (так как белых и чёрных шляп по две штуки, то если бы на втором и третьем были бы две одинаковые шляпы, первому бы не хватило такой же, так как одинаковых шляп всего по две и третьей одинаковой нет)). Так что второй тут же поймёт, что на нём белая шляпа, и скажет об этом. Это и есть ответ задачи.
После этого третий поймёт, что раз на нём не такая шляпа, как на втором, а на втором белая, значит, на нём чёрная, и тоже скажет об этом.
Первый и так это знал, так что ему от этого не станет ясно, какая шляпа на нём. А пока первый не узнает, не узнает и четвёртый. Так что ни первый, ни четвёртый так и не узнают, какие на них шляпы. НИКОГДА.
Точнее, пока не снимут их и не посмотрят. :) Вот так.
Вы снова не правы, внимательнее читайте условие, никто кроме второго не сможет узнать цвет шляпы.
Смотри если б я стоял бы на месте первого я сказал бы что на мне черная шляпа!
Речь идет о освобождение не было б времени думать чередуются шляпы или нет.
А что если всë пойдет не по плану и первый скажет, что на нем чëрная шляпа следуя банальной логики чередующихся цветов?
а если спросят сначала 4-го? а потом 3-го? а где в условиях сказано, что они слушают что говорит предыдущий? им задали аопрос какая на тебе шляпа? и никаких дебатов там нет.
А где в условии задачи сказано что шляпы чередуются.... ??? если бы было сказано что шляпы чередуются, тогда ответ могут найти Первый и Второй, а так ответа нет...
Первыми догадаются 1-ый и 2-ой.Потому что 1-ый видит 2 и 3.У второго шляпа белая а у 3 черная,а тут и может догодатся в какой он шляпе.2-ой видит 3-го который в черной шляпе значит он в белой шляпе. xD Надеюсь что правильно.
Или вообще снять и посмотреть... В условии нет что нельзя трогать шляпу))
верно! молодец!
А что если 1ый специально ничего не говорит, чтобы 2ой не догадался
Первый видит двух в шляпах разного цвета. На вопрос в какой он шляпе он говорит "не знаю" так как еще остаются 1 белая и 1 черная. второй человек слышит ответ первого и понимает что он не знает потому что перед ним шляпы разного цвета. Впереди 2ой видит парня с черной шляпой, поэтому понимает что у него белая.
Четвертый первым угадает свой цвет. Потому что в загадке написано что перед четвертым есть перегородка и никто ниче не видит. А четвертый может снять шляпу и узнать свой цвет так как никто ничего не видит
первый
а вот я угадал) потому что наподобие этой головоломки была другая,там всё объяснили
Легкая задача!!!
vse otveti ne verniye, tak kak perviy videt 2 i 3 on nacenayet dumat i naxodet otvet 4to u nevao cernoya shlapa na eto idet neskolko sekund 4tobi podumat, a 4-iy voabwey necevo ne videt i otvecaet "ne znayu" pervim, a vopros bil kto otvetit pervim:)))
Нет, четвёртый первым не ответит - он будет ждать ответа первого. Ведь если первый точно назовёт свою шляпу, то это будет значить, что первый видит перед собой две одинаковые шляпы и, следовательно на четвёртом и на первом шляпы тоже одинаковые. Рассуждая дальше, приходим к выводу, что все будут ждать ответа первого, ведь только после того как он ответит, у них появится возможность больше узнать о своей шляпе. Таким образом, получается, что первым ответит (если других не спросят раньше) участник под номером 1. :)
1й первым не ответит, потому что допускаются только 2 варианта ответа. Угадывать не допустимо. А так как 1й видит 1 белую и 1 черную шляпу, то он ответит: "Нет. Не знаю". И из этого ответа 2й сделает логичный вывод(если он конечно не дурак, в смысле 2й, а не вывод) и получит лвл-ап, встанет на ступеньку выше, таким образом замыкая круг. В результате все они умрут.
если спросят сначала второго, то тогда первый ответит в какой он шляпе
второй и первый одновременно
так как первый видит что ближе к нему белая шляпа значит он в чёрной
а второй видит перед собой чёрную шляпу а значит он в белой
"Одновременно..." - такой ответ в этой задаче не предусмотрен. Объясню почему. Во-первых, в условии ясно сказано, что спрашивают каждого из них, т.е. не всех сразу. Во-вторых, если отвечать будут все наперебой, задача сведется к соревнованию "Кто быстрее сможет произнести вслух без ошибок название горы в Новой Зеландии..." И в третьих, стрелочка на рисунке как бы однозначно намекает на последовательность опроса.
Est toka odin otvet, dorogie Dami i gospoda.
Pervim uznaet tot, kto rezvee, i imenno, kto shljapu pervim snimet.
так как тут надо додумывать шо они могут слышать друг друга. можно следующее обозначить: допустим второй глухой, а первый ответил на языке глухонемых так как он хитрый и тому подобное... вариантов может быть масса
Это было бы сказано в условии.
Чудаки надели шляпы, даже не знают какие!
Тот кто первый додумается шляпу снять! А вообще согласитесь странно, что 4-х взрослых людей загнали в помещение, надели на них шляпы,а перед одним даже стенку поставили. Хотя ответов много!!!
не впадай в крайность. не в этом суть. Суть в том чтобы правильно размышлять
я думаю что 4-ый потомучто говорят что через стенку ни чего не видно но не говорят что через нее ни чего не слышно !)
тут сказано что они знают как стоят(чередование тоже предполагаем), знают сколько шляп белых и черных, поэтому второй может сделать предположение, что если перед ним стоит человек с черной шляпой, то и сзади тоже. Поэтому он в белой шляпе.
Тупость! Первый может просто сказать цвет второго и все! если бы была задача, чтобы все сказали свой цвет - то да!
Но в задаче и нужно сказать СВОЙ цвет.
если ты не можешь решить задачу, это ещё не значит что эта задача - "тупость".
Внимательно читай условия: Допускается два варианта ответа: "Да, знаю, я в ... шляпе" либо "Нет. Не знаю".
Есть еще один альтернативный ответ - никто не сможет ответить в какой он шляпе.
Все из-за неправильно поставленного вопроса.
Каждого из них спрашивают: "Знаешь ли ты, в какой ты шляпе?"
1. Можно подразумевать, что каждого из них спрашивают так, чтобы никто не слышал их ответ.
2. Спросить могут всего один раз, и не указано в каком порядке (если 2-го человека спросят раньше первого, то ответ в задаче будет альтернативным)
Соглашусь только во втором случае, если бы они говорили шёпотом, то это было бы сказано в условии задачи
Даже если 2 спросят раньше 1 никто из них не поймет в какой он шляпе пока 2 не скажет в какой он шляпе(если не случай когда 2 и 3 в шляпах одного цвета и 1 сразу может ответить,в этом случае все могут назвать цвет своей шляпы), а 2 этого не скажет пока не узнает ответ 1.
Страницы