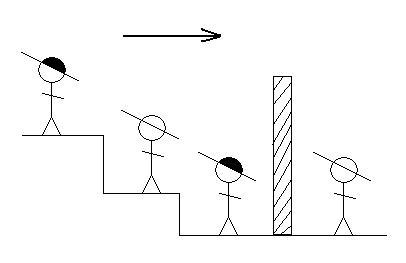
На этом рисунке 4 человека, двое из них в черных шляпах и двое - в белых.
Перегородка - это стена, через которую ничего не видно.
Слева направо: 1-й человек видит 2-го и 3-го, 2-й видит 3-го, 3-й видит стенку, 4-й вообще ничего не видит.
Они знают, как они стоят, знают, что есть 2 черные и 2 белые шляпы.
Каждого из них спрашивают: "Знаешь ли ты, в какой ты шляпе?"
Допускается два варианта ответа: "Да, знаю, я в ... шляпе" либо "Нет. Не знаю"
Кто первым сможет ответить, в какой он шляпе?
Ответ: Второй.

Комментарии
Второй. Читайте "Опубликовано Макс в Сб, 03/03/2012 - 21:36"
очень круто!я 4 клас!
ЕСЛИ ОНИ РАЗГОВАРИВАЮТ НЕ ПОВАРАЧИВАЯСЬ! То 1 КРИЧИТ: Я ВИЖУ БЕЛУЮ ШЛЯПУ И ЧЕРНУЮ ШЛЯПУ!
2 КРИЧИТ: Я ВИЖУ ЧЕРНУЮ ШЛЯПУ
3 КРИЧИТ: ЗНАЧИТ Я В ЧЕРНОЙ ШЛЯПЕ
слева-направо. 1-ый - я не знаю., 2-ой - услышав это понимает, что у него и у 3-его шляпы разные и отвечает первым. справа-налево. 4-ый - я не знаю., 3-ий - я не знаю., 2-ой - я не знаю., 1-ый - я не знаю и до 2-ого сразу доходит: если 1-ый не знает, значит у меня с 3-им шляпы разные и отвечает первым. Кстати и последним, после его правильного ответа никто больше всё равно не сможет сказать цвет своей шляпы.
неверно последнее утверждение. после второго третий ответит, т.к. знает, что он со вторым в разных шляпах
Товарищи бунтари ,не могу с вами согласиться.Задача составлена вполне коректно.Кстати, получается могут назвать двое свои цвета в такой последовательности:2,3.
как третий блин что ты тупиш.он тока стену видит и ответ тока первый потому что он видит второго и
3 значит он понимает что за стенкой в белой а он в чёрной.
В ответе к задаче же сказано, что первый может думать, что они розставлены "Чорный, Белый,Чорный, Белый" или "Белый, Белый, Чорный, Чорный".
А третий может дать ответ только после ответа второго. Он должен разсуждать так:"На 2-ом белая шляпа. Если бы на мне тоже была белая, то 1-ый бы сразу сказал, что на нем черная, однако он молчит. Значет у меня(3-его) и 2-ого шляпы разные. Раз на нем белая, то на мне чорная."
Обратите внимание на рисунок! (Высоко сижу далеко гляжу) Только первый может знать в какой он шляпе.
konechno vtoroy....2 stoit v centre,on smotrit vniz i vidit chto u 3 chyornaya shlyapa a tak kak oni stoyat posledovatelno to vixodit chto on v beloy.............
второй, потому что он видит черную шляпу перед собой, а стоящий позади если бы видел две черные шляпы перед собой, он ответил бы что у него белая методом исключения, но т.к. первый молчит второй понимает что у него не черная а белая.
Самый разумный ответ
не точно
Если рассуждать по логике, то ответ в точности до 100% - это ответ 2 - ой. Все потому что если рассуждать по логике, человек 1 - ый не может сказать точно, что он в черной, потому что посмотрев вперед он может подумать, что последовательность шляп может быть не чередующей. К примеру - Белый, Белый, Черный, Черный. Из этого следует, что второй посмотрев вперед и увидев черную шляпу, может предположить, что либо за ним черная, либо впереди, а то есть за стеной черная, из этого можно уверено сказать, что 2 скажет точно, если он не дурак)))
Читайте внимательно!!! Каждый видит только одного человека, 2-й видит только 3-го
нет правильного ответа на этот вопрос. потому что 2ой не знает последовательности и на обязательно что он подумает именно так как вы написали. а на счет "есль он не дурак" то просто он может рассуждать более обширно нежели Вы.
из условия "1-й человек видит 2-го и 3-го"
1-й видит две различные шляпы=>не может сказать в какой он
2-й слышит что грит 1-й, значит он (2-й) и 3-й в разных шляпах => видит черную(на 3-ем) => значит он (2-й) в белой
ответ: Второй
Абсолютно верно! Это единственное и достаточное рассуждение.
прочитай №9
загадка для дураков
тут нельзя уверенно сказать в какой ты шляпе
только время потратил зря
и 2 ответ тоже неверный
тут вообще нет правильного ответа
Это очень просто! Правильный ответ - это 2й человечек он догадался в какой он шляпе! Как? Очень просто 4й находится за стеной и не видит ни кого и он говорит (не знаю), 3й человек видя перед собой черную и белую тоже говорит не знаю так как на нем может быть и черная и белая, а 2й человек слыша за спиной ответ (не знаю) догадывается какой цвет его шляпы т.е 2й видит черную шляпу, а 3й промолчал значит 3й человек видит разные шляпы и не знает и 2й конечно же догадывается какая у него шляпа!
по такому способу ,Евлашов, - если 2-ой догадывается в какой он шляпе по сзади чёрному и впереди чёрному,почему 3-ий не может догадаться по 1-ому чёрному и 2-ому белому?(чёрный,белый,черный)
Я думаю что здесь не точного ответа нет.
Дурак здесь только ты. почитай мой коммент под первым постом.
Правильного ответа нет! Так как в условии не сказано, в каком смысле они знают, как они стоят!!! Конкретизируйте, пожалуйста!
1)В задаче нигде не указано что шляпы чередуются
2)Правильный ответ 2,3
1 задают вопрос, он видит перед собой белую и черную шляпу, соответственно он говорит незнаю.
2 задают вопрос, он видит черную шляпу и знает ответ первого, учитывая, что первый ответил не знаю значит у него шляпа с 3 разного цвета, он отвечает белая.
3 задают вопрос, он не видит нечего, но знает что ответили 1 и 2, второй ответил белая а первый не незнаю, значит у него со вторым шляпы разные, его ответ черная
Правильный ответ - второй. Потому что надо назвать не всех кто свой цвет поймет а только первого.
но должен быть 3...................а почему 2???
2-й человек первый скажет в какой он шляпе, если не дурак. Он видит только черную, то есть вероятность что он в белой шляпе 2/3 по отношению к черной 1/3. Для первого вероятность угадать цвет 1/2. Для 3 и 4 вероятность угадать 1/4. Также следует отметить если он услышит ответ первого "не знаю" то вероятность того что он в белой 100%.
Здесь нет места никаким вероятностям!!! Со 100% гарантией второй человек может сказать, что у него белая шляпа. Ход его рассуждений таков: На человеке впереди меня (3-й человек) черная шляпа. Ели бы на мне была тоже черная шляпа, то 1-й человек сразу же отгадал бы цвет своей шляпы. Но поскольку 1-й молчит, значит на мне БЕЛАЯ шляпа. Вот и весь ход рассуждений
а первый не молчит (по условию) - не надо сюда тупо переписывать решения подобных задач
Второй человек. Первый не может определить в какой именно он шляпе. Он ответит "Нет. Не знаю". Второй, учитывая то, что первый не знает цвета своей шляпы, догадывается, что у него самого и третьего человека шляпы разного цвета (если бы они были одинаковы, то первый человек мог бы ответить на вопрос о цвете своей шляпы). Соответственно, видя цвет шляпы третьего человека, второй человек быстрее всех сможет ответить, в какой он шляпе.
На самом деле задача с поставлена некорректно и ответа на нее нету, никто не догадается: ибо 1 видит двоих и не знает в какой он шляпе, когда у второго спрашивают он видит только одного, и не знает в какой шляпе сам, А в условии не сказано что второй человек слышал что ответит первый, соответственно он не знает что тот ответил и не может ни о чем догадываться,
Корректнее было бы составлять задачу так:
Слева на право каждого спрашивают: "в какой ты шляпе?" Человек может ответить:
"да я в ... шляпе" или "не знаю". Если человек отвечает: "да, я в ... шляпе" допрос заканчивается.
В таком случае будет логично понятно что если вопрос дошел ко второму значит он сделал вывод о том что они с 3им в разных шляпах и методом исключения определил. А не так как поставлена задача тут.
Это же очень просто.. Первый говорит "не знаю". из этого Второй делает вывод что они с третьим в разных шляпах(потому что если бы они были в одинаковых то первый бы смог назвать свой цвет шляпы) и говорит что в белой(потому что видит перед собой черную шляпу)
проще всего по теории вероятности, первый видит две шляпы разного цвета, значит он знает, что его шансы 50 на 50, третий не видит никого, его шансы тоже 50 на 50, так как половина шляп чёрные и половина белые, в той же ситуации четвёртый; а вот второй видит лишь одну шляпу чёрного цвета, то есть ему надо угадать цвет своей, при условии, что имеется две белых и одна чёрная, то бишь шансы того, что он в белой - 66 к 33, как то так
Для такого ответа нужно совсем по-другому сформулировать условие
в условиях нет уточнения о том, в какой последовательности их спрашивают (могут и с 4 начать) и нет уточнения, слышат ли они ответ соседа.
Может быть и первый, если впереди стоят в одинаковых шляпах. А вот если впереди в разных,
то тогда второй. Задача не правильна составлена.
Давайте вас поставим в такие условия. Вы стоите вторым. И первый раз вам надели черную (вам об этом не сказали), потом вам стерли в памяти информацию об этой загадке, и второй раз вам надели уже белую шляпу. Два раза вы первее всех догадаетесь какого цвета у вас шляпа?
Вообще задание на самом деле некорректное. Не сказано в условии, что они будут слушать друг друга, да и не сказано в каком порядке их опрашивают. Возможно первого спросят последним. А если в условии не определено то тогда можно сказать что 4 снимет шляпу и посмотрит. А может подует ветер шляпы слетят. Если нет всех условий, то задача некорректная. Я не должен попадать мыслями с тем кто составлял задачку и додумывать условия необходимые для ответа. По условия 4 не видит никого вариант шляпы 50 на 50. Соответственно 3 также. Первый видит по одной шляпе, соответственно вероятность шляпы также 50 на 50, а у второго вероятность белой шляпы 66% против 33% черной. То есть на 100% никто не может сказать какая у него шляпа, но у второго вероятность угадать свою выше.
Идиотизм какой-то,а не логическая задача))Они,что изначально не знали в каких они шляпах стоят??Что за идиот вообще придумал эту задачу?
Мой ответ на эту задачу прост : Вопрос был в том что "кто назовёт цвет своей шляпы первым?" То есть не обязательно верно назвать так что мне кажется что 4 назовёт первым свой цвет шляпы так как у него шанс угадать 50 на 50 и ему терять нечего так как он знает что за ним стена и даже развернутся и посмотреть у него нет возможности так что из за безвыходной ситуации он ответит первым не зависимо от того правильно он назвал цвет шляпы или нет....
Нет ответа ! По условиям никто не может узнать какого цвета у них шляпа!!! Даже если сли первый крикнет что не знает какого цвета у него шляпа ето ничего не даст ну а если крикнет цвет тогда каждый поймет какой у кого цвет!! И что за бред за второго как он может узнать вы почитайте свои ответы! Путаете людей!!!
Логика шпионов - у меня есть своя версия :) писать долго :) но попробую чуть позже.
а может и не ответить
Никогда никто не ответит правильно, т.к. ни второй ни третий не знают что они второй и третий. Никто из них не знает что четвертый за стеной. Соответственно будут думать что третий это четвертый а второй это третий или второй это первый а третий это второй и двое за стеной. В вопросе же не написано что у каждого будут спрашивать называя его номер. Соответственно никто не ответит никогда.
Страницы